Gauß auf Java
Ein mathematischer Reisebericht

Fünfeck, Siebzehneck und 257-Eck

Über das Dreieck und das Quadrat sagen wir in diesem Kapitel nichts..

Das Fünfeck

Für das regelmäßige Fünfeck gibt das Programm die folgende Darstellung aus (die numerische Vereinfachung bei $p_{1,0}$ und $p_{1,1}$ wurde hier und in den folgenden Darstellungen von Hand ergänzt). 

% Running with arguments: 5 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1+\sqrt{5}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1-\sqrt{5}}{2}\]
% 1/2 * p_{1,0} = 0.30901699437494745
% cos(2*pi/5): 0.30901699437494745
% Time used: 0.019803774sec

Wenn man die Ausgabe mit LaTeX aufbereitet ergibt sich: \[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1+\sqrt{5}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1-\sqrt{5}}{2}\]

Abb.1: Konstruktion des regelmäßigen Fünfecks
[Bild in neuem Tab anzeigen]

Es musste also nur überall der Wert $-1$ für $p_{0,0}$ eingesetzt werden und man erhält: \[\cos(2\pi/5) = \frac{1}{2}p_{1,0} = \frac{-1 + \sqrt{5}}{4}\]

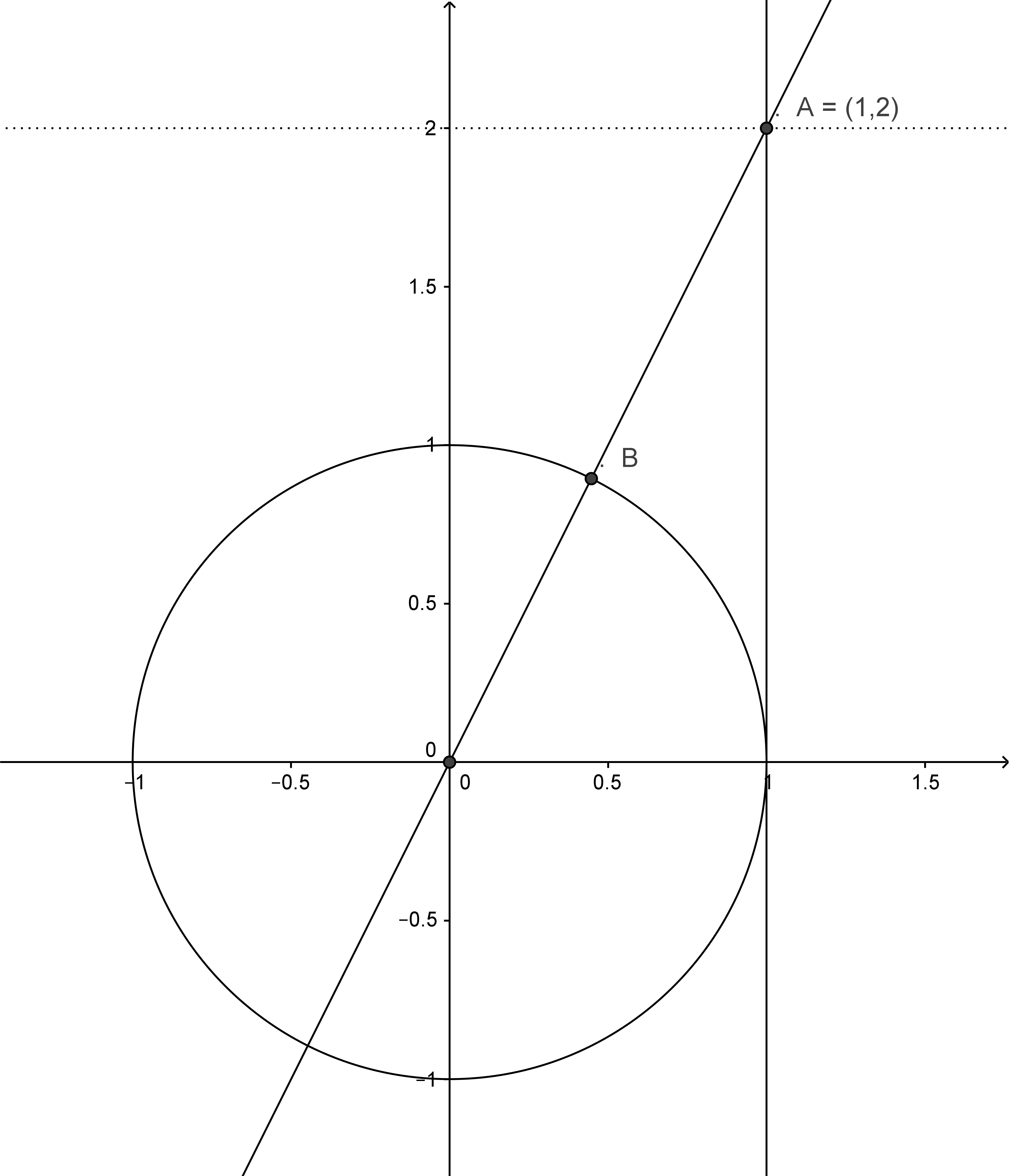
Hier, wie bei allen anderen Konstruktionen, besteht der erste Schritt darin, die Wurzel aus der Eckenzahl zu ziehen, davon $1$ zu subtrahieren und das Ergebnis zu halbieren. Beim Fünfeck ist damit, nach einer weiteren Halbierung, alles erledigt. Man beachte, dass $\sqrt{5}$ die Länge der Hypotenuse in einem rechtwinkligen Dreieck mit den Katheten $1$ und $2$ ist. Davon wird die kürzere Kathetenlänge abgezogen, man hat hier die übliche Konstruktion zum Goldenen Schnitt, wie in Abb.1 angedeutet. Die $x$-Koordinate der Einheitswurzel $\zeta^1_5$ erhält man durch Vierteln der Strecke $AB$.

Das Siebzehneck

Für das regelmäßige Siebzehneck ist die Ausgabe: 

% Running with arguments: 17 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1+\sqrt{17}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1-\sqrt{17}}{2}\]
\[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\]
\[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]
\[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]
% 1/2 * p_{3,0} = 0.9324722294043557
% cos(2*pi/17): 0.9324722294043558
% Time used: 0.022387692sec

Mit LaTeX aufbereitet: \[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1+\sqrt{17}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1-\sqrt{17}}{2}\] \[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\] \[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\] \[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\] \[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\] \[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\] \[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]

Hier sind die Ersetzungen etwas komplizierter, aber es lässt sich immer noch ein einigermaßen übersichtlicher geschlossener Ausdruck angeben:

\[p_{3,0} = \tfrac{1}{2}p_{2,0} + \tfrac{1}{2}\sqrt{p_{2,0}^2 - 4(p_{2,1})}\] $$ \begin{align*} p_{3,0} &= \tfrac{1}{4}\bigg(p_{1,0} + \sqrt{p_{1,0}^2 -4(-1)}\bigg) \\ &+ \tfrac{1}{2}\sqrt{\bigg( \frac{p_{1,0} + \sqrt{p_{1,0}^2-4(-1)}}{2}\bigg)^2 - 4\bigg(\frac{p_{1,1} + \sqrt{p_{1,1}^2 -4(-1)}}{2}\bigg)} \end{align*} $$ $$ \begin{align*} p_{3,0} &= \tfrac{1}{4}\bigg(\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2 -4(-1)}\bigg) \\ &+ \tfrac{1}{2}\sqrt{\bigg( \frac{\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2-4(-1)}}{2}\bigg)^2 - 4\bigg(\frac{\frac{-1 - \sqrt{17}}{2} + \sqrt{\big(\frac{-1 - \sqrt{17}}{2}\big)^2 -4(-1)}}{2}\bigg)} \end{align*} $$ Die obigen Ausdrücke wurden durch schematisches Suchen und Ersetzen im Editor erzeugt. Mit etwas Rechenaufwand ließe sich der Ausdruck weiter vereinfachen, hier sollen aber nur die einfachsten Ersetzungen durchgeführt werden. Wir geben gleich den Wert für $\cos(2\pi/17) = 1/2 \cdot p_{3,0}$ an: $$ \begin{align*} \cos(2\pi/17) &= \tfrac{1}{8}\bigg(\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2 +4}\bigg) \\ &+ \tfrac{1}{4}\sqrt{\bigg( \frac{\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2+4}}{2}\bigg)^2 - 4\bigg(\frac{\frac{-1 - \sqrt{17}}{2} + \sqrt{\big(\frac{-1 - \sqrt{17}}{2}\big)^2 +4}}{2}\bigg)} \end{align*} $$ Dieser Term lässt sich mit Geduld und einem Taschenrechner ausrechnen: $$ \begin{align*} \cos(2\pi/17) &= \tfrac{1}{8}\left(1.56155 + \sqrt{\left(1.56155\right)^2 +4}\right) \\ &+ \tfrac{1}{4}\sqrt{\left( \frac{1.56155 + \sqrt{\left(1.56155\right)^2+4}}{2}\right)^2 - 4\left(\frac{-2.56155 + \sqrt{\left(2.56155\right)^2 +4}}{2}\right)} \end{align*} $$ \[ \cos(2\pi/17) = \tfrac{1}{8}(1.56155 + 2.53740) + \tfrac{1}{4}\sqrt{( \frac{1.56155 + 2.53740}{2})^2 - 4(\frac{-2.56155 + 3.2498}{2})}) \] \[ \cos(2\pi/17) = \tfrac{1}{8}\cdot 4.09895 + \tfrac{1}{4}\sqrt{( \frac{4.09895}{2})^2 - 4(\frac{0.68825}{2})} \] \[ \cos(2\pi/17) = \tfrac{1}{4}(2.049475 + \sqrt{4.20034 - 1.3765}) \] \[ \cos(2\pi/17) = 0.932476 \]

Der Wert stimmt im Rahmen der Rechengenauigkeit mit dem durch das Programm fortlaufend berechneten Wert überein. Die oben abgeleiteten Wurzelausdrücke lassen sich im Prinzip direkt als Konstruktionsanweisung für das $17$-Eck benutzen. Im Laufe der Zeit wurde die eigentliche Konstruktion immer wieder vereinfacht, oder es wurden zusätzliche Bedingungen gestellt. Bei einer Suche nach 17-Eck  oder 17-gon  findet man im Internet zahlreiche Beispiele. Eine systematische, wenn auch etwas ältere Darstellung verschiedener Konstruktionsverfahren bietet [Mitzscherling 1913].

Das 257-Eck

Perioden, die für die Berechnung von $p_{7,0}$ nicht gebraucht werden, sind mit Hilfe des Programms Kompressor aus der Originalausgabe entfernt worden. 

% Running with arguments: 257 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1+\sqrt{257}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1-\sqrt{257}}{2}\]
\[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\]
\[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,2} = \tfrac{p_{2,2} + \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,6} = \tfrac{p_{2,2} - \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,1} = \tfrac{p_{2,1} - \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\]
\[p_{3,5} = \tfrac{p_{2,1} + \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\]
\[p_{3,3} = \tfrac{p_{2,3} - \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\]
\[p_{3,7} = \tfrac{p_{2,3} + \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\]
\[p_{4,0} = \tfrac{p_{3,0} + \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\]
\[p_{4,8} = \tfrac{p_{3,0} - \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\]
\[p_{4,4} = \tfrac{p_{3,4} + \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\]
\[p_{4,12} = \tfrac{p_{3,4} - \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\]
\[p_{4,2} = \tfrac{p_{3,2} + \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\]
\[p_{4,10} = \tfrac{p_{3,2} - \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\]
\[p_{4,6} = \tfrac{p_{3,6} - \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\]
\[p_{4,14} = \tfrac{p_{3,6} + \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\]
\[p_{4,1} = \tfrac{p_{3,1} + \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,9} = \tfrac{p_{3,1} - \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,5} = \tfrac{p_{3,5} + \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,13} = \tfrac{p_{3,5} - \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,3} = \tfrac{p_{3,3} + \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,11} = \tfrac{p_{3,3} - \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,7} = \tfrac{p_{3,7} + \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,15} = \tfrac{p_{3,7} - \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{5,0} = \tfrac{p_{4,0} + \sqrt{p_{4,0}^2 - 4(p_{4,0}+p_{4,2}+p_{4,1}+p_{4,5})}}{2}\]
\centerline{\footnotesize 2 unreferenced roots were skipped}
\[p_{5,24} = \tfrac{p_{4,8} + \sqrt{p_{4,8}^2 - 4(p_{4,8}+p_{4,10}+p_{4,9}+p_{4,13})}}{2}\]
\centerline{\footnotesize 12 unreferenced roots were skipped}
\[p_{5,1} = \tfrac{p_{4,1} + \sqrt{p_{4,1}^2 - 4(p_{4,2}+p_{4,6}+p_{4,1}+p_{4,3})}}{2}\]
\centerline{\footnotesize 2 unreferenced roots were skipped}
\[p_{5,25} = \tfrac{p_{4,9} + \sqrt{p_{4,9}^2 - 4(p_{4,10}+p_{4,14}+p_{4,9}+p_{4,11})}}{2}\]
\centerline{\footnotesize 9 unreferenced roots were skipped}
\[p_{5,23} = \tfrac{p_{4,7} + \sqrt{p_{4,7}^2 - 4(p_{4,8}+p_{4,12}+p_{4,9}+p_{4,7})}}{2}\]
\[p_{5,15} = \tfrac{p_{4,15} + \sqrt{p_{4,15}^2 - 4(p_{4,0}+p_{4,4}+p_{4,1}+p_{4,15})}}{2}\]
\centerline{\footnotesize 1 unreferenced roots were skipped}
\[p_{6,0} = \tfrac{p_{5,0} + \sqrt{p_{5,0}^2 - 4(p_{5,1}+p_{5,23})}}{2}\]
\centerline{\footnotesize 6 unreferenced roots were skipped}
\[p_{6,56} = \tfrac{p_{5,24} + \sqrt{p_{5,24}^2 - 4(p_{5,25}+p_{5,15})}}{2}\]
\centerline{\footnotesize 56 unreferenced roots were skipped}
\[p_{7,0} = \tfrac{p_{6,0} + \sqrt{p_{6,0}^2 - 4(p_{6,56})}}{2}\]
\centerline{\footnotesize 1 unreferenced roots were skipped}
% 1/2 * p_{7,0} = 0.9997011578431021
% cos(2*pi/257): 0.9997011578430937
% Time used: 0.104295518sec
Used: 40; Skipped: 89; Roots: 7144

Man sieht, dass im Rahmen der Rechengenauigkeit der aus den Wurzelausdrücken sukzessiv berechnete Wert mit dem direkt über Cosinus berechneten Wert übereinstimmt.

Wir quälen MathJax ein wenig und lassen auch diese Wurzeln aufbereiten, schenken uns aber die Ersetzungen, wie wir sie beim Siebzehneck durchexerziert haben. Der Grund dafür folgt weiter unten. Da MathJax nur LaTex-Ausdrücke innerhalb einer Mathe-Umgebung rendert, bleiben die eingeschobenen Textblöcke unreferenced notes were skipped unaufbereitet, was aber hoffentlich niemanden stört.

\[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1+\sqrt{257}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1-\sqrt{257}}{2}\] \[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\] \[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,2} = \tfrac{p_{2,2} + \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,6} = \tfrac{p_{2,2} - \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,1} = \tfrac{p_{2,1} - \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\] \[p_{3,5} = \tfrac{p_{2,1} + \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\] \[p_{3,3} = \tfrac{p_{2,3} - \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\] \[p_{3,7} = \tfrac{p_{2,3} + \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\] \[p_{4,0} = \tfrac{p_{3,0} + \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\] \[p_{4,8} = \tfrac{p_{3,0} - \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\] \[p_{4,4} = \tfrac{p_{3,4} + \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\] \[p_{4,12} = \tfrac{p_{3,4} - \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\] \[p_{4,2} = \tfrac{p_{3,2} + \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\] \[p_{4,10} = \tfrac{p_{3,2} - \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\] \[p_{4,6} = \tfrac{p_{3,6} - \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\] \[p_{4,14} = \tfrac{p_{3,6} + \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\] \[p_{4,1} = \tfrac{p_{3,1} + \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,9} = \tfrac{p_{3,1} - \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,5} = \tfrac{p_{3,5} + \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,13} = \tfrac{p_{3,5} - \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,3} = \tfrac{p_{3,3} + \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,11} = \tfrac{p_{3,3} - \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,7} = \tfrac{p_{3,7} + \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,15} = \tfrac{p_{3,7} - \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{5,0} = \tfrac{p_{4,0} + \sqrt{p_{4,0}^2 - 4(p_{4,0}+p_{4,2}+p_{4,1}+p_{4,5})}}{2}\] \centerline{\footnotesize 2 unreferenced roots were skipped} \[p_{5,24} = \tfrac{p_{4,8} + \sqrt{p_{4,8}^2 - 4(p_{4,8}+p_{4,10}+p_{4,9}+p_{4,13})}}{2}\] \centerline{\footnotesize 12 unreferenced roots were skipped} \[p_{5,1} = \tfrac{p_{4,1} + \sqrt{p_{4,1}^2 - 4(p_{4,2}+p_{4,6}+p_{4,1}+p_{4,3})}}{2}\] \centerline{\footnotesize 2 unreferenced roots were skipped} \[p_{5,25} = \tfrac{p_{4,9} + \sqrt{p_{4,9}^2 - 4(p_{4,10}+p_{4,14}+p_{4,9}+p_{4,11})}}{2}\] \centerline{\footnotesize 9 unreferenced roots were skipped} \[p_{5,23} = \tfrac{p_{4,7} + \sqrt{p_{4,7}^2 - 4(p_{4,8}+p_{4,12}+p_{4,9}+p_{4,7})}}{2}\] \[p_{5,15} = \tfrac{p_{4,15} + \sqrt{p_{4,15}^2 - 4(p_{4,0}+p_{4,4}+p_{4,1}+p_{4,15})}}{2}\] \centerline{\footnotesize 1 unreferenced roots were skipped} \[p_{6,0} = \tfrac{p_{5,0} + \sqrt{p_{5,0}^2 - 4(p_{5,1}+p_{5,23})}}{2}\] \centerline{\footnotesize 6 unreferenced roots were skipped} \[p_{6,56} = \tfrac{p_{5,24} + \sqrt{p_{5,24}^2 - 4(p_{5,25}+p_{5,15})}}{2}\] \centerline{\footnotesize 56 unreferenced roots were skipped} \[p_{7,0} = \tfrac{p_{6,0} + \sqrt{p_{6,0}^2 - 4(p_{6,56})}}{2}\] \centerline{\footnotesize 1 unreferenced roots were skipped}

Auf der Webseite [Winter 2011] findet man Links zu Videos, die die Konstruktion eines 257-Ecks mit Hilfe eines Geometrieprogramms vorführen. Auch die Wikipedia enthält eine Animation zur Konstruktion des 257-Ecks.

Interessant ist noch die Ausgabe Roots: 7144 des Programms Kompressor. Das Programm zählt nämlich mit, wie viele Quadratwurzeln in dem endgültigen Ausdruck auftauchen würden, wenn alle Ersetzungen der $p_{m,n}$ wie oben beim Siebzehneck vorgenommen würden. Damit ist klar, warum wir auf diese Übung hier verzichten. Der Wert 7144 weicht etwas von dem Wert ab, der in [Trott 2000] angegeben wird. Trott kommt nämlich auf 5133 Wurzeln. Die einzige Erklärung, die ich dafür anbieten kann, ist der Hinweis auf die Überlegenheit von Mathematica®, was die Algorithmen zur Vereinfachung der Wurzelausdrücke angeht. Die Routine simplify im Programm Hermes ist ja schon als primitiv klassifiziert worden. Es kann natürlich sein, dass der Kompressor einen Programmierfehler enthält. Falls jemand einen solchen entdeckt, wäre ich für eine kurze Mitteilung dankbar.